Understanding Compounding
Definition of Compounding
Compounding is the process in which an asset's
earnings (e.g. capital gains or interest) are reinvested to generate
additional earnings over time. This growth, referred to as compound growth,
occurs at an exponential rate because the investment generates earnings from
both the principal (original amount) and the accumulated earnings (which
increase over time). Hence, the term compound
which means
combined
(i.e. the combined growth from two or more parts, in this
case, the principal and the accumulated earnings).
Sometimes compound growth is referred to as compound interest
,
exponential growth
, or compounding returns
—all of these
terms mean the same thing.
Simple vs. Compound Growth
Compound growth is contrasted with linear growth, or simple growth. Simple growth occurs when only the principal generates earnings.
Two scenarios will be explored to help illustrate the effect of compounding, along with the difference between simple and compound growth.
Scenario 1: Simple Growth
Say that there is an investment that returns 5% annually and an individual decides to invest $100 for thirty (30) years. In the first year, the investment returns $5, in the second year, it also returns $5 and this continues for thirty (30) years, returning a total of $150 over the duration.
| Amount Invested | Earnings | |
|---|---|---|
| Year 1 | $100.00 | $5.00 |
| Year 2 | $100.00 | $5.00 |
| Year 3 | $100.00 | $5.00 |
| ... | ... | ... |
| Year 30 | $100.00 | $5.00 |
| Total | $100.00 | $150.00 |
Scenario 2: Compound Growth
Continuing with the same parameters as before: a 5% annual return and an investment horizon of thirty (30) years. However, this time the earnings each year are reinvested to generate additional earnings.
- In the first (1) year, the investment returns only $5 as before, but this $5 is reinvested.
- In the second (2) year, the investment, now worth $105, returns $5.25 ($5 from the principal and 25c from the reinvested earnings).
- Fast forward to the tenth (10) year, and the investment is now worth $155.13 and returns $7.76.
- Finally, in year thirtieth (30) year, the investment is worth $411.61 and returns $20.58 for a total return of $332.19 over the thirty years.
| Amount Invested | Earnings | |
|---|---|---|
| Year 1 | $100.00 | $5.00 |
| Year 2 | $105.00 | $5.25 |
| Year 3 | $110.25 | $5.51 |
| ... | ... | ... |
| Year 10 | $155.13 | $7.76 |
| ... | ... | ... |
| Year 30 | $411.61 | $20.58 |
| Total | $432.19 | $332.19 |
Earnings Comparison
It is evident from these two scenarios that by reinvesting earnings and allowing the returns to compound, one is able to generate significantly higher gains than what would be possible with a simple growth investment. Over the thirty years, the 5% Rate of Return (RoR) generated only $150 in simple interest, but $332.10 in compound interest (over double the earnings). While this difference may seem substantial, it becomes more pronounced as the rate of return increases. For example, if the rate of return was 7% over those thirty (30) years, the investment would have produced $210 in simple interest, but $661.23 in compound interest (more than triple the earnings). If you bump up the rate of return again to 9%, one earns over four and a half times the money, and at 11% the difference increases to over six and a half times.
| RoR | Simple Earnings | Compound Earnings | Rel. Earnings Inc. |
|---|---|---|---|
| 5% | $150.00 | $332.19 | 2.21x |
| 7% | $210.00 | $661.23 | 3.15x |
| 9% | $270.00 | $1226.77 | 4.54x |
| 11% | $330.00 | $2189.23 | 6.63x |
Importance of Duration
At first it may seem like the Rate of Return (RoR) is the only important parameter to prioritise when it comes to compound growth, however, the other critical variable is the investment duration. If an investment is not given sufficient time to let earnings/growth accumulate, then the full power of compounding is not utilised. This is best highlighted by plotting the growth of investments over thirty (30) years with varying rates of return.
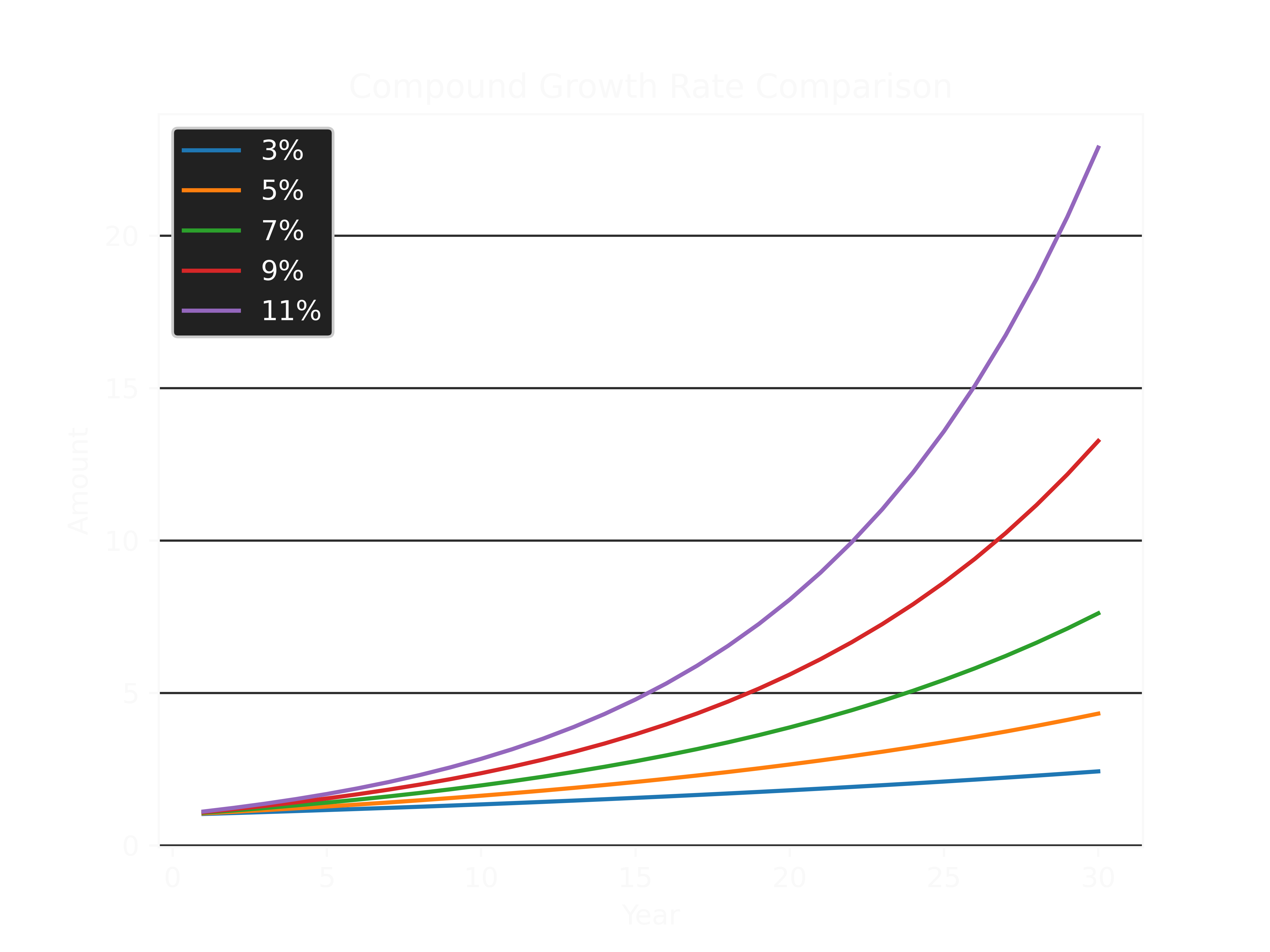
From the graph, it can be seen that the major divergence in overall returns between the different RoRs manifests after approximately ten (10) years. Prior to that, the difference is relatively small. Therefore, as a general rule of thumb, investors in most circumstances should be aiming for the longest holding period possible, preferably one that is greater than 10 years in order to maximise the effect of the compounding process.
Summary
Compounding is defined as the process in which an asset's earnings are reinvested to generate additional earnings over time. This growth, referred to as compound growth, occurs at an exponential rate because the investment generates earnings from both the principal (original amount) and the accumulated earnings (which increase over time). This is contrasted with simple growth in which only the principal generates earnings.
Both the rate of return and investment duration are key variables that determine the effectiveness of the compounding process. As a general rule of thumb, holding periods longer than ten (10) years are preferred, and the rate of return should be as high as reasonably attainable. With that being said, most people will see the large gains made possible by high RoRs and immediately seek these higher rates without understanding that they necessarily come with a higher level of risk. Risk is a complex topic which be covered in another lesson linked below, but for now it is important to remember that chasing high RoRs without consideration for the inherent risk will, under most circumstances, lead to poor long-term performance.